función cubica
Una función cúbica es una función polinómica de grado 3. Las funciones cúbicas tienen expresiones del tipo:
Estamos interesados en estudiar la derivada de funciones simples con un punto de vista intuitivo y visual. Para estudiar la derivada de una función cúbica vamos a seguir la misma aproximación que hemos usado para el caso de las funciones cuadráticas.
EL CONCEPTO DE DERIVADA DE UNA FUNCIÓN
La derivada de una función en un punto puede definirse como la tasa de variación instantánea o como la pendiente de la recta tangente a la gráfica de la función en ese punto. Podemos definir la pendiente de la función en un punto como la pendiente de la recta tangente.
La pendiente de la tangente depende, en general, de x. Entonces, a partir de una función podemos definir una nueva función, la función derivada de la función original.
El proceso de encontrar la función derivada de una función se llama diferenciación.
El valor de la función dericada para cada valor de x es la pendiente de la función original en x.
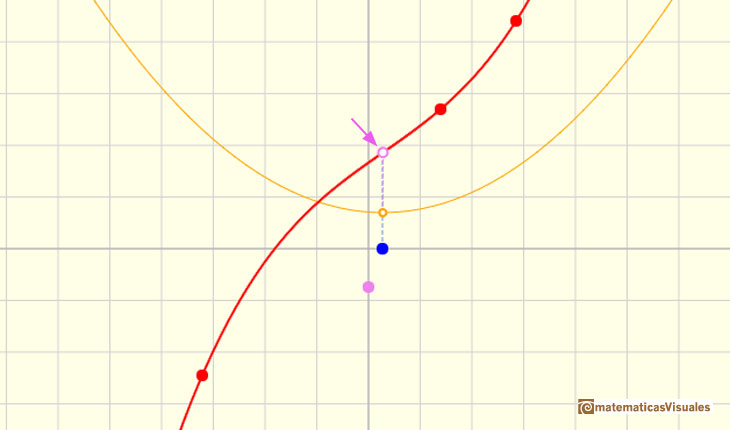
Para representar la derivada en un punto podemos dibujar la recta tangente a la gráfica de una función cúbica en ese punto:
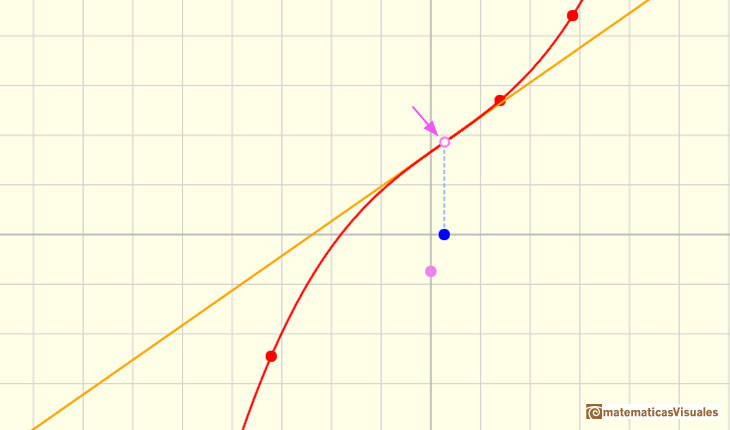
Pero, ¿cómo podemos dibujar la tangente? Podemos usar una lupa. Si miramos muy cerca el punto en la gráfica de la función podemos ver cómo la recta tangente es muy semejante a la función. La recta tangente es la mejor aproximación lineal de la función en ese punto:
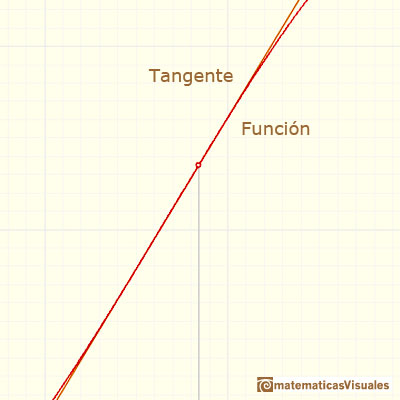
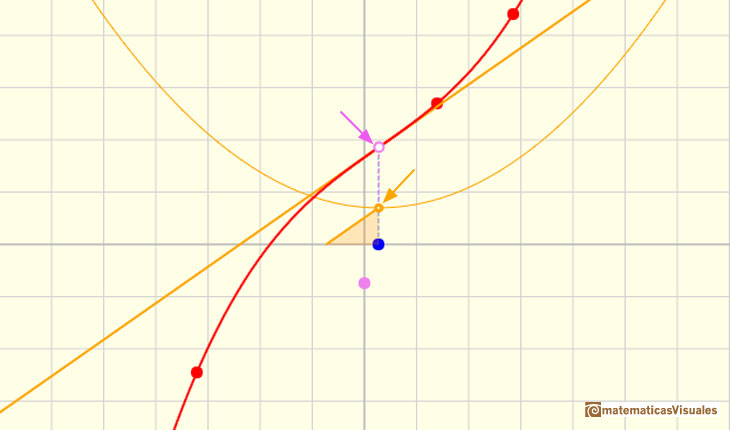
Entonces podemos dibujar una recta paralela a esta tangente a través del valor x-1 y obtenemos un triángulo rectángulo:
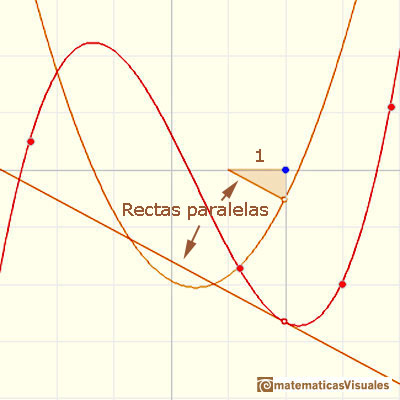
La derivada de una función cúbica es una función cuadrática.
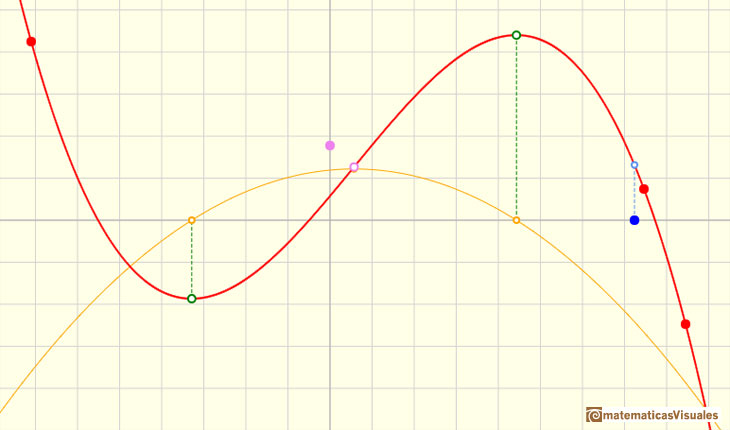
Un punto crítico es un punto en el que la tangente es paralela al eje de abcisas (eje x). Es decir, que la pendiente de la recta tangente en ese punto es 0.
En el siguiente ejemplo podemos ver una función cúbica con dos puntos críticos. Uno es un máximo local y el otro es un mínimo local. En estos puntos, la función derivada (una parábola) corta al eje x:
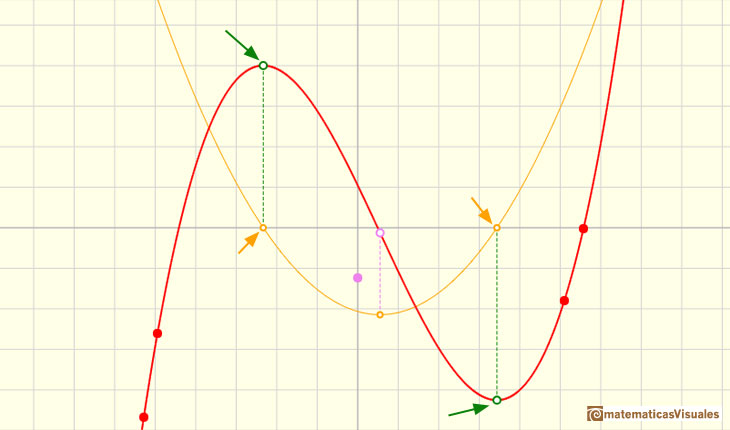
Estos puntos críticos son puntos en los que la función deja de crecer o decrecer (también se les llama puntos estacionarios). En estos puntos, la recta tangente es horizontal.
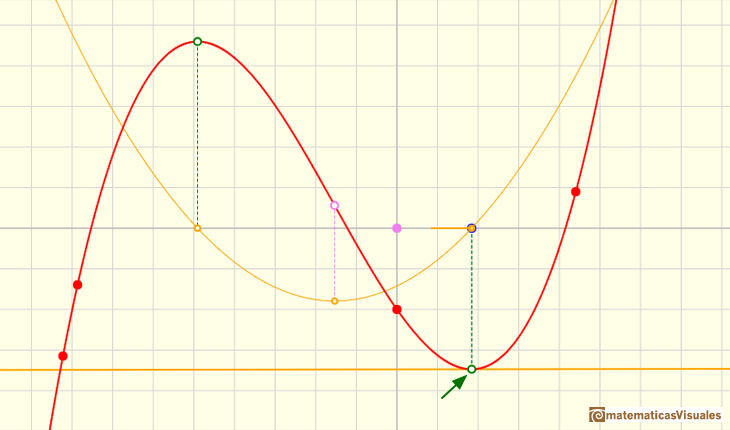
Para encontrar los puntos estacionarios podemos resolver la ecuación cuadrática:
En este caso, las soluciones de esta ecuación son:
Como ya sabemos (funciones cuadráticas), algunas ecuaciones cuadráticas no tienen soluciones reales (la parábola no corta al eje de las x). En estos casos la función cúbica no tiene puntos críticos:
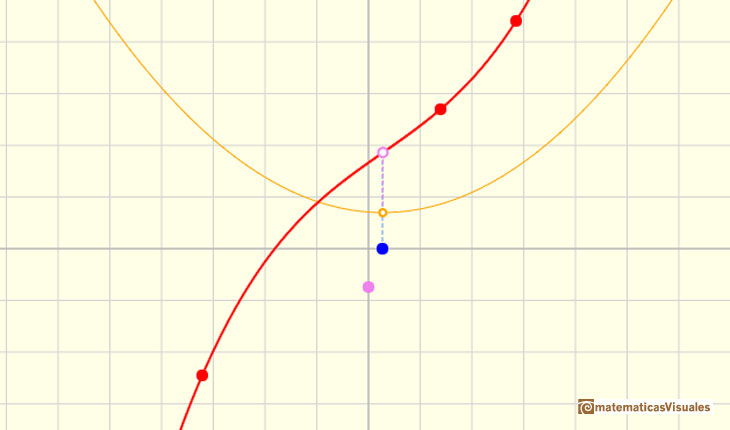
Pero una parábola siempre tiene un vértice. El vértice de la parábola está relacionado con un punto de la función cúbica. Llamamos a este punto un punto de inflexión.
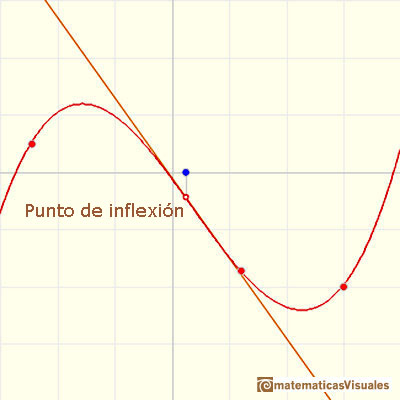
Un punto de inflexión de una función cúbica es el único punto de la gráfica en el que cambia la concavidad.
La curva cambia de ser cóncava hacia arriba a ser cóncava hacia abajo, o viceversa.
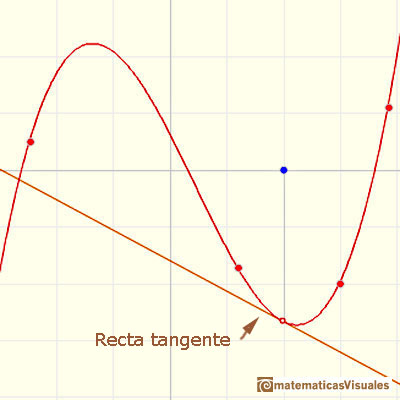
La recta tangente a una función cúbica en el punto de inflexión cruza la gráfica:
Para calcular el punto de inflexión podemos calcular el vértice de la parábola:
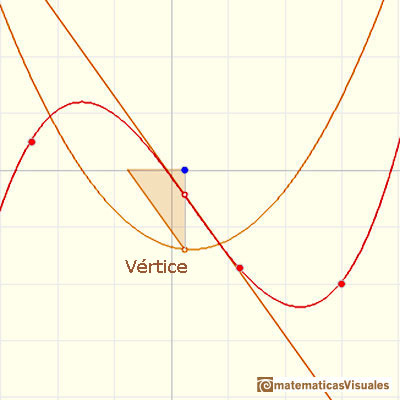
Este es un ejemplo de un punto de inflexión de una función cúbica que no tiene puntos críticos: